
Une lentille convergente est caractérisée par son centre optique O par lequel passe l’axe optique de la lentille Δ, son foyer image F’ et son foyer objet F (F est symétrique de F par rapport à O). L’axe optique Δ est orienté dans le sens de propagation de la lumière.
Pour déterminer graphiquement l’image d’un objet par une lentille convergente, il est nécessaire de tracer trois rayons particuliers issus d’un point B de cet objet, B étant situé hors de l’axe optique.
Après avoir traversé la lentille, ces rayons se croisent en un point B’ qui est l’image de B par la lentille. On reconstitue l’image A’B’ de l’objet en traçant A’B’.
1️⃣ Compléter le tracé des rayons
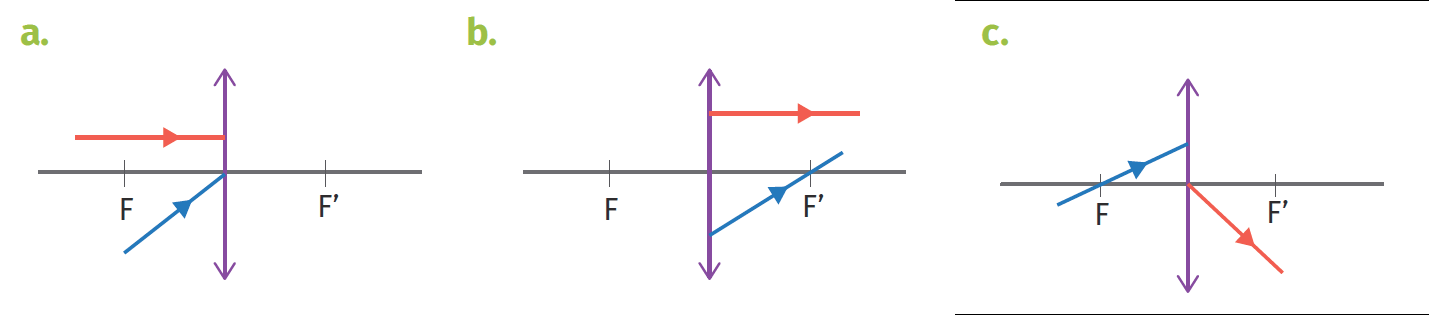
3 rayons particuliers et leurs
caractéristiques|<ul><li>celui qui passe par O n'est pas dévié<li>celui qui passe par F' émerge parallèlement à l'axe optique<li>celui qui arrive parallèle à l'axe optique émerge en F</ul>
Une image est droite lorsqu’elle est
dans le même sens que l’objet et renversée
lorsqu’elle est dans le sens inverse.
Une image est réelle lorsqu’elle est
obtenue par le croisement direct des rayons et virtuelle lorsqu’elle est obtenue par le
croisement du prolongement de rayons.
3 caractéristiques d’une
image|<ul><li>droite / renversée<li>plus petite, grande ou de même taille que l'objet<li>réelle ou virtuelle</ul>
2️⃣ Construction de l’image A’B’.
\(\overline{AB}\) = -3
\(\overline{BA}\) = 3
Par convention les grandeurs sont positives vers la droite et
vers le haut.
L’image A’B’ est réelle si OA’ >
0.
L’image A’B’ est virtuelle si OA’ < 0
.
La distance focale de la lentille est notée \(\overline{OF'}\) (ou \(f'\)) . Elle se mesure en mètre. Pour une lentille convergente : \(\overline{OF’} > 0\).
Le grandissement permet de comparer la taille et l’orientation de l’image à celle de l’objet.
▶️ Exercice : détermination du grandissement et des caractéristiques de l’image
3️⃣ Thalès et interprétation des valeurs de \(γ\)
Le théorème de Thalès nous permet d’écrire :
\[\frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{OA'}}{\overline{OA}}\]
ou avec les notations du livre :
\[\frac{y_{B'}}{y_B} = \frac{x_{A'}}{x_A}\]
formule du grandissement γ|\[\frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{OA'}}{\overline{OA}}\] ou \[\frac{y_{B'}}{y_B} = \frac{x_{A'}}{x_A}\]
Si \(\gamma > 0\) : l’objet et l’image sont dans le même sens
Si \(\gamma < 0\) : l’objet et l’image sont dans des sens opposés
Si \(\lvert\gamma\rvert > 1\) :
l’image est plus grande que l’objet
Si \(\lvert\gamma\rvert < 1\) :
l’image est plus petite que l’objet
Relation de conjugaison de Descartes
\[\frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}} = \frac{1}{\overline{OF'}}\]
avec les notations du livre :
\[\frac{1}{x_{A'}} - \frac{1}{x_A} = \frac{1}{f'}\]
▶️ Application de la formule de conjugaison
relation de conjugaison|\[\frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}} = \frac{1}{\overline{OF'}}\] ou \[\frac{1}{x_{A'}} - \frac{1}{x_A} = \frac{1}{f'}\]
4️⃣ Exercices d’application
Correction